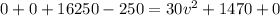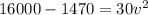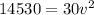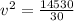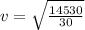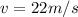Answer:
22m/s
Step-by-step explanation:
Mass, m=60 kg
Force constant, k=1300N/m
Restoring force, Fx=6500 N
Average friction force, f=50 N
Length of barrel, l=5m
y=2.5 m
Initial velocity, u=0
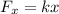
Substitute the values

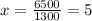 m
m
Work done due to friction force
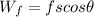
We have

Substitute the values
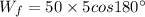
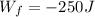
Initial kinetic energy, Ki=0
Initial gravitational energy,
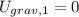 \
\
Initial elastic potential energy
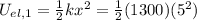
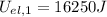
Final elastic energy,
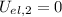
Final kinetic energy,
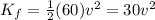
Final gravitational energy,
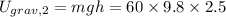
Final gravitational energy,
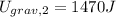
Using work-energy theorem
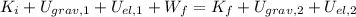
Substitute the values