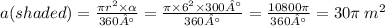Question

PLEASE HELP IM STRUGGLING!!

And please answer in fraction form

The circle below has center O, and its radius is 6 m. Given that m ZAOB=60°, find the length of the arc ADB and the area of the shaded region.
Give exact answers in terms of , and be sure to include the correct units in your answer.

Answer 1

arc ADB = 10π m

A (shaded) = 30π m^2

Explanation:

Given:

∠AOB = 60° (it is a central angle, which is equal to the arc on which it rests on)

r (radius) = 6 m

Find: arc ADB - ? A (shaded) - ?

If arc AB is 60°, then arc ADB is (remember, that a full circle forms an angle of 360°):

`\alpha = 360° - 60° = 300°`

Now, we can find the length of the arc ADB:

`l = (2\pi * r * \alpha )/(360°) = (2\pi * 6 * 300°)/(360°) = (3600\pi)/(360°) = 10\pi \: m`

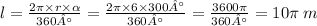
The shaded region is a cutout of a circle

We can find its area by using this formula:

`a(shaded) = \frac{\pi {r}^(2) * \alpha }{360°} = \frac{\pi * {6}^(2) * 300°}{360°} = (10800\pi)/(360°) = 30\pi \: {m}^(2)`