Question

I need some help with some homework;

The graph shows the relationship between the number of months different students practiced baseball and the number of games they won:

The title of the graph is Baseball Games. On x axis, the label is Number of Months of Practice. On y axis, the label is Number of Games Won. The scale on the y axis is from 0 to 22 at increments of 2, and the scale on the x axis is from 0 to 12 at increments of 2. The points plotted on the graph are the ordered pairs 0, 1 and 1, 3 and 2, 5 and 3, 9 and 4, 10 and 5, 12 and 6, 13 and 7, 14 and 8,17 and 9, 18 and 10,20. A straight line is drawn joining the ordered pairs 0, 1.8 and 2, 5.6 and 4, 9.2 and 6, 13 and 8, 16.5 and 10, 20.5.
Part A: What is the approximate y-intercept of the line of best fit and what does it represent? (5 points)

Part B: Write the equation for the line of best fit in slope-intercept form and use it to predict the number of games that could be won after 13 months of practice. Show your work and include the points used to calculate the slope. (5 points)

Answer 1

Part A: The y-intercept of the line of best fit is 0. This means that for zero months of practice, the team should expect not to win a game.

Part B: y = 2.11429x

Explanation:

y = 2.11429(13)

y ≈ 27 games

You give some points that say it makes a straight line, but it doesn't.

Helping in the name of Jesus.

Answer 2

let's move like the crab, backwards, so let's do B) first.

to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below, keeping in mind that those points are as close as possible to the best-fit line, so they can pretty much define it

`(\stackrel{x_1}{6}~,~\stackrel{y_1}{13})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{17}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{17}-\stackrel{y1}{13}}}{\underset{\textit{\large run}} {\underset{x_2}{8}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ 2 } \implies 2`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{13}=\stackrel{m}{ 2}(x-\stackrel{x_1}{6}) \\\\\\ y-13=2x-12\implies {\Large \begin{array}{llll} y=2x+1 \end{array}}`

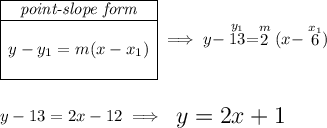
after 13 months of practice, so x = 13, thus

`y = 2(\stackrel{x }{13}) + 1 \implies y=27\qquad \textit{possible games won by then}`

now, onto A) well hmm the best-fit line equation is already in slope-intercept form, so the y-intercept is simply (0 , 1), the heck does that mean?

means that with "0" practice, the students can only beat one team or win only "1" time.