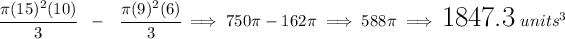Question

Trapezoid PQRS is formed when right triangle TPQ is cut by line SR such that

SR || PQ. Find the volume of the solid generated when the trapezoid is rotated
about side SP. Round your answer to the nearest tenth if necessary.

Answer 1

Check the picture below.

so if we rotate the triangle TPQ abou the side PT we'll end up with a cone with a radius of 15 and a height of 10 as you see there, now, using the triangle STR about the side ST we'd end up with a smaller cone of radius 9 and height of 6.

So let's get the volume of each cone and subtract the volume of the smaller cone from that of the larger cone, and what's leftover is, you guessed it, the volume of the trapezoid, the part that wasn't subtracted.

`\stackrel{ \textit{\LARGE larger} }{\textit{volume of a cone}}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ r=15\\ h=10 \end{cases}\implies V=\cfrac{\pi (15)^2(10)}{3} \\\\\\ \stackrel{ \textit{\LARGE smaller} }{\textit{volume of a cone}}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ r=9\\ h=6 \end{cases}\implies V=\cfrac{\pi (9)^2(6)}{3} \\\\[-0.35em] ~\dotfill`

`\cfrac{\pi (15)^2(10)}{3}~~ - ~~\cfrac{\pi (9)^2(6)}{3}\implies 750\pi -162\pi \implies 588\pi\implies \text{\LARGE 1847.3}~units^3`