Question

I need to know what is the step in finding the answer

Answer 1

z = -1.5

6.68%

More than 2.5 standard deviations: X > 125 mg/dl

Less than 2.5 standard deviations: X < 75 mg/dl

Explanation:

If a continuous random variable X is normally distributed with mean μ and variance σ², it is written as:

`\boxed{X \sim\text{N}(\mu,\sigma^2)}`

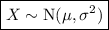
Given:

• Mean μ = 100 mg/dl
• Standard deviation σ = 10 mg/dl

Therefore, if the blood sugar levels are normally distributed:

`\boxed{X \sim\text{N}(100,10^2)}`

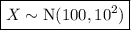
where X is the blood sugar level in milligrams per deciliter.

Converting to the Z distribution:

`\boxed{\textsf{If }\: X \sim\textsf{N}(\mu,\sigma^2)\:\textsf{ then }\: (X-\mu)/(\sigma)=Z, \quad \textsf{where }\: Z \sim \textsf{N}(0,1)}`

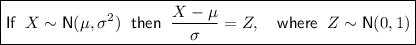
If David has a blood sugar of 85 mg/dl then X = 85:

`\implies Z=(85-100)/(10)=-1.5`

To calculate the percentile, find the area associated with the z-score on the Z Table (attached). Multiply the area by 100 and add a percentage sign:

`z=-1.5 \implies 0.0668=6.68\%`

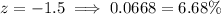
The calculations of the blood sugar readings that would be more than or less than 2.5 standard deviations from the mean are:

`\implies \mu + 2.5 \sigma=100+2.5(10)=100+25=125`

`\implies \mu -2.5 \sigma=100-2.5(10)=100-25=75`

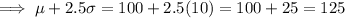
The blood sugar readings that would be more than 2.5 standard deviations from the mean are:

• Readings that are more than 125 mg/dl: X > 125

The blood sugar readings that would be less than 2.5 standard deviations from the mean are:

• Readings that are less than 75 mg/dl: X < 75