Question

What is the area of this polygon? Enter your answer in the box. units² K Q Search ​

Answer 1

45 units²

Explanation:

You want the area of the figure comprised of a triangle atop a rectangle.

Composite area

The area of the whole will be the sum of the areas of the parts. Here, we can decompose the figure into a rectangle of width 5 -(-4) = 9 units and height -2 -(-4) = 2 units.

The triangle above the rectangle has the same base width, and height 4 -(-2) = 6 units.

The total area is ...

`A = bh_r +(1)/(2)bh_t\qquad\text{$h_r$=rectangle height; $h_t_$=triangle height}\\\\A=b(h_r+(1)/(2)h_t)= 9(2+(6)/(2))=9\cdot5=45`

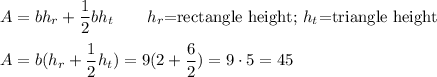
The area of the polygon is 45 units².

__

Additional comment

When finding the area of composite figures, we often find it useful to treat the area of a triangle as equal to the area of a rectangle of the same width and half the height, or the same height and half the width.

You can figure the area other ways, too. You can subtract the triangle corner areas from the 9 wide by 8 high enclosing rectangle. You can draw a vertical line through N and divide the figure into two trapezoids with bases 2 and 8. Or, you can simply add the areas of rectangle and triangle after computing them separately.