Answer:

Explanation:
To convert our function
 to the vertex form, we must express it in the following form:
to the vertex form, we must express it in the following form:
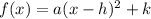
where:
 vertical compression
vertical compression
 horizontal traslation
horizontal traslation
 vertical translation
vertical translation
To convert the function, I will look for a square binomial that gives me the first two terms of our function.
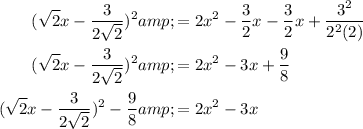
Now, I substitute
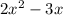

Hope it helps