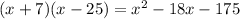Question

Factor the polynomial, if possible. If the expression cannot be factored, enter the expression as is.

Answer 1

Explanation:

Here we have a quadratic polynomial which has a general form:

`ax^2+bx+c` ;

A quadratic polynomial can be factored into product of two linear polynomials as:
`(x-a_1)(x-a_2)=x^2-(a_1+a_2)x+a_1* a_2` .

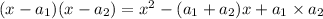In our case
`a=1, b=-18, c=-175`.

Which implies that
`a_1+a_2=18\ and \ a_1* a_2=-175`. Now 25 times -7 is equal to -175 and sum of 25 and -7 is 18 which can perfectly fit our description so we can say that
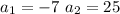`a_1=-7 \ a_2=25`. Hence we can factorize our equation as:

`(x+7)(x-25)=x^2-18x-175`