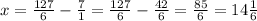Question

Find two mixed number so that the sum is 21 1/6 and the difference is 43/6

Answer 1

`7 \: \: and \: \: 14 (1)/(6)`

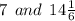
Explanation:

Assume, the 1st mixed number is x and the 2nd one is y

Let's write 2 equations according to the given information:

`x + y = 21 (1)/(6)`

`x - y = (43)/(6)`

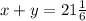
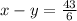
Let's make x the subject from the 1 equation:

`x = 21 (1)/(6) - y`

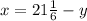
Replace x in the 2nd equation with its value from the 1st one:

`( 21(1)/(6) - y) - y = (43)/(3)`

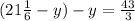
Eliminate the brackets and collect like-terms:

`- 2y = (43)/(6) - 21 (1)/(6)`

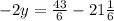
Convert the number 21 1/6 to an improper fraction:

`- 2y = (43)/(6) - (21 * 6 + 1)/(6)`

`- 2y = (43)/(6) - (127)/(6) = ( - 84)/(6)`

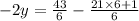
Multiply both sides of the equation by 6 to eliminate the fraction:

`- 12y = - 84`

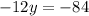
Divide both sides of the equation by -12 to make y the subject:

`y = 7`

`x = (127)/(6) - (7)/(1) = (127)/(6) - (42)/(6) = (85)/(6) = 14 (1)/(6)`