Question

Below, quadrilateral ABCD is plotted with coordinates A(0,8), B(4,2), C(-3,-4) and D(-7,2). (a) Calculate the slope of each line segment. Show your calculation and express your answers in simplest form. AB BC: CLASS ACTIVITY Calculate the slope of each line segment. Show your calculation and express your answers in simplest form. CD: AD: (b) What conclusions can you make about parallel sides based on these slope calculations?

Answer 1

(a) The slope of each line segment is given by;

AB = -3/2.

BC = 6/7.

CD = -3/2.

AD = 6/7.

(b) Quadrilateral ABCD is a parallelogram because sides AB and CD are parallel sides and sides BC and AD are parallel sides.

In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;

Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)

Slope (m) = rise/run

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

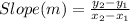
Part a.

For segment AB, we have:

Slope (m) AB = (2 - 8)/(4 - 0)

Slope (m) AB = -6/4

Slope (m) AB = -3/2

For segment BC, we have:

Slope (m) BC = (-4 - 2)/(-3 - 4)

Slope (m) BC = -6/-7

Slope (m) BC = 6/7

By substituting the given data points C (-3,-4) and D (-7,2) into the formula for the slope of a line, the slope of segment CD is given by;

Slope (m) CD = (2 - (-4))/(-7 - (-3))

Slope (m) CD = -6/4

Slope (m) CD = -3/2

By substituting the given data points A (0,8) and D (-7,2) into the formula for the slope of a line, the slope of segment AD is given by;

Slope (m) AD = (2 - 8)/(-7 - 0)

Slope (m) AD = -6/-7

Slope (m) AD = 6/7

Part b.

In this context, we can logically deduce that sides AB and CD are parallel sides while sides BC and AD are parallel sides because their slopes are the same. Therefore, quadrilateral ABCD is a parallelogram.