Question

Line L has equation y= -x-2. Find the distance between L and the point A(6,-1)

round answer to the nearest tenth

Answer 1

• 5.0 units

------------------------------

We need to find the distance between line L and point A(6, -1).

To find the distance d between the point and the line, we'll use the point-to-line distance formula, which is given by:

`d = ( |Ax + By + C| )/(√(A^2 + B^2) )`

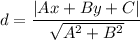
where, A, B, and C are the coefficients of the line Ax + By + C = 0.

For line L, we have the equation y = - x - 2, which can be rewritten as:

• x + y + 2 = 0, therefore, A = 1, B = 1, and C = 2.

The coordinates of point A are x = 6, y = - 1.

Now we can plug these values into the formula:

`d = ( |1*6 + 1*(-1) + 2| )/(√(1^2 + 1^2) )=(|7|)/(√(2) ) =(7)/(√(2) ) =5.0`

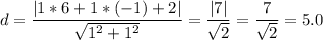
So, the distance between line L and point A(6, -1) is approximately 5.0 units, rounded to the nearest tenth.