Question

The ph of an aqueous solution of 0.287 m ammonium iodide, nh4i (aq), is . this solution is

Answer 1

The pH of an aqueous ammonium iodide solution will be acidic due to the formation of hydronium ions by the ammonium ion, NH4+. Calculating the specific pH would require knowledge of the molarity and the acid dissociation constant of NH4+.

Step-by-step explanation:

The pH of an aqueous solution of ammonium iodide, NH4I (aq), will be acidic. This is because the ammonium ion (NH4+) is the conjugate acid of the weak base ammonia (NH3) and ionizes in water to produce hydronium ions (H3O+), leading to an acidic solution. The acid dissociation constant (Ka) of the ammonium ion (NH4+) is 5.6 × 10-10, illustrating its tendency to donate a proton to water. If we were to calculate the pH of a specific concentration of NH4Cl, similar to our original compound, we would use the concentration of the ammonium ion to set up an ICE table and solve for the concentration of hydronium ions, then use the pH formula pH = -log[H3O+]. For the case of NH4I, if we know the molarity and the acid dissociation constant, we can similarly calculate the pH.

Answer 2

The pH of a 287 M aqueous solution of ammonium iodide is approximately 5.51, indicating that the solution is acidic.

The pH of a solution can be calculated using the concentration of hydrogen ions
`(\(H^+\))` in the solution. Ammonium iodide
`(\(NH_4I\))` is a salt that dissociates in water into its constituent ions: ammonium
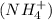`(\(NH_4^+\))` and iodide
`(\(I^-\))` ions.

The ammonium ion
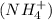`(\(NH_4^+\))` is acidic because it can donate a proton
`(\(H^+\))` in water:

`\(NH_4^+ \rightarrow NH_3 + H^+\)`

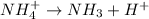
The concentration of
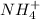`\(NH_4^+\)` ions in a 287 M solution of ammonium iodide is 287 M. To find the pH, you can calculate the concentration of
`\(H^+\)` ions produced by the dissociation of
`\(NH_4^+\)`.

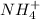However, to accurately calculate the pH, you need to consider the dissociation constant
`(\(K_a\))` of ammonium ion
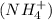`(\(NH_4^+\))` in water, which is approximately
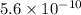`\(5.6 * 10^(-10)\)`. Using this dissociation constant, you can calculate the concentration of
`\(H^+\)` ions formed from the dissociation of
`\(NH_4^+\)`.

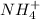Let's calculate the pH:

Given: Concentration of
`\(NH_4^+\) = 287 M`

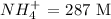
The equation for the dissociation of ammonium ion is:

`\(NH_4^+ \rightarrow NH_3 + H^+\)`

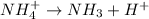
The
`\(K_a\)` expression for this dissociation is:

`\(K_a = ([NH_3][H^+])/([NH_4^+]) = 5.6 * 10^(-10)\)`

Given that the initial concentration of
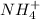`\(NH_4^+\)` is 287 M and assuming negligible contribution from water:

Let x be the concentration of
`\(H^+\)` ions formed. Since the dissociation is 1:1:

`\(K_a = (x * x)/(287)\)`

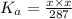
Solving for x:

`\(x = √(K_a * 287)\)`

`\(x = \sqrt{5.6 * 10^(-10) * 287}\)`

`\(x \approx 3.1 * 10^(-6)\)`

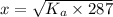
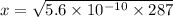
So, the concentration of
`\(H^+\)` ions formed from the dissociation of
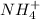`\(NH_4^+\)` is approximately
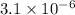`\(3.1 * 10^(-6)\)` M.

Using the definition of pH:

`\(pH = -\log[H^+]\)`

`\(pH = -\log(3.1 * 10^(-6))\)`

`\(pH \approx 5.51\)`

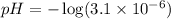
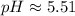
Therefore, The answer is approximately 5.51.

The complete question is here:

What is the PH of a 287 M м aqueous solution of ammonium Iodide, NH 4 I ? PH : is the solution (acidic, basic, neutral)