Question

A car m = 2050 kg is traveling at a constant speed of v = 26 m/s. the car experiences a drag force (air resistance) with magnitude fd = 260 n.

a. Write an expression for the power the car must produce Pi to maintain its speed.
b. What is the power in horsepower (hp)?
c. The car encounters an incline which makes an angle of θ = 6 degrees with respect to the horizontal. The cruise control kicks in and increases the power to maintain the speed of the car. What is the new power (in hp) required to maintain a constant speed?

Answer 1

To maintain a constant speed, the car must produce power equal to the sum of the drag force and the force of friction. The power can be calculated using the formula Pi = (Fd + Ff) * v. When the car encounters an incline, the power required to maintain a constant speed increases.

Step-by-step explanation:

To maintain a constant speed, the car must produce power equal to the sum of the drag force and the force of friction. The power Pi can be calculated using the formula:

Pi = (Fd + Ff) × v

where Fd is the drag force, Ff is the force of friction, and v is the velocity of the car.

To find the power in horsepower (hp), you can convert the power Pi from watts (W) to horsepower using the conversion factor 1 hp = 746 W.

When the car encounters an incline, the power required to maintain a constant speed increases. The new power can be calculated using the same formula, but with an additional force component due to the incline. The new power can then be converted to horsepower as before.

Answer 2

The car must produce a power of 6760 W, or about 9.06 hp, to maintain its speed against the drag force. On an incline with a 6° angle, the new power required is approximately 61412 W or 82.3 hp to maintain the same speed.

Given:

m = 2050 kg

v = 26 m/s

Drag force,
`f_(d)` = 260 N

(a) The power P required to maintain a constant speed is given by the product of force and velocity:

`\[ P = F \cdot v \]`

where F is the force applied, and v is the velocity.

P = 260 x 26 = 6760 W

(b) To convert the power from watts to horsepower, you can use the conversion factor:

1 hp = 746 W

`\[ P_{\text{HP}} = (260 \, \cdot 26 \, )/(746 \ ) \]` = 9.06 hp

(c) When the car encounters an incline, the additional force required to counteract the component of gravity along the incline is given by:

`\[ F_{\text{gravity}} = m \cdot g \cdot \sin(\theta) \]`

Given:

θ = 6 degrees

g = 9.8 m/
`s^(2)`

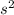
`\[ F_{\text{gravity}}` = 2050 x 9.8 x sin 6° = 2102 N

The total force
`\( F_{\text{total}} \)` is the sum of the drag force and the component of gravity along the incline:

`\[ F_{\text{total}} = F_{\text{drag}} + F_{\text{gravity}} \]` = 260 + 2102 = 2362 N

The new power
`\(P_{\text{new}}\)` required is then given by:

`\[ P_{\text{new}} = F_{\text{total}} \cdot v \]` = 2362 x 26 = 61412 W

In horsepower,

`\(P_{\text{new}}\)` =
`(61412)/(746)` = 82.3 hp

The values vary with the angle of incline.