Question

Can someone please explain to me how to get the distance? i don't understand, thank you! ​

Answer 1

Slopes

SE: 0 EN: 3

TN: 0 ST: 3

Distances (Lengths)

SE: 7 EN: 2
`√(10)`

TN: 7 ST: 2
`√(10)`

Explanation:

Slopes

The slope of SE and TN is 0, as over any period of x, the lines' y-value does not increase. Thus, their slope can be represented as:

rise / run = 0 / ∞ = 0

The slope of EN and ST is 3.

rise / run = 3 / 1 = 3

Note that the slope of opposite sides is the same because opposite sides of a parallelogram are parallel.

Distances

The distance of SE and TN is the same thing as their length. We can see that these sides are both 7 units long.

Note that the length of opposite sides is the same because opposite sides of a parallelogram are congruent.

The distance of EN and ST can be solved for using the Pythagorean Theorem. We can create a triangle with side EN or ST as its hypotenuse and apply the theorem to that triangle.

The triangle's dimensions are: length = 6, width = 2

Plugging into the Pythagorean Theorem and solving for SE:

`a^2 + b^2 = c^2`

`6^2 + 2^2 = EN^2`

`36 + 4 = EN^2`

`EN = √(40)`

`EN = √( 2 \cdot 2 \cdot 10)`

`EN = 2√(10)`

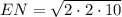
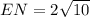
So, EN and ST are both 2
`\bold{√(10)}` units long.