Final Answer:
The maximum error in approximating
 by the expression
by the expression
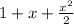 when
when
 is approximately
is approximately
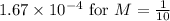 . This estimation is based on the Remainder Estimation Theorem, which considers the third derivative of
. This estimation is based on the Remainder Estimation Theorem, which considers the third derivative of
 and utilizes a value of
and utilizes a value of
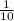 to represent the interval of interest. Thus the correct option is A. The maximum error is approximately
to represent the interval of interest. Thus the correct option is A. The maximum error is approximately
 .
.
Step-by-step explanation:
The Remainder Estimation Theorem states that if f(x) is approximated by the Taylor series
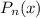 up to the nth term, then the remainder
up to the nth term, then the remainder
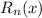 is given by:
is given by:
![\[R_n(x) = (f^((n+1))(c))/((n+1)!) \cdot (x-a)^(n+1)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/znkvvjo7ju9l2y09b8lgu6ikhm3blz2upp.png)
where (c) is between (a) and (x). In this case, the approximation is
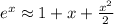 , and we want to estimate the error when \
, and we want to estimate the error when \
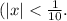
The Remainder Estimation Theorem helps us bound the error term by finding the maximum value of
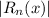 for (x) in the given interval. For our approximation, the third derivative of
for (x) in the given interval. For our approximation, the third derivative of
 is
is
 , and we take (M) as
, and we take (M) as
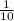 because we're interested in the interval where
because we're interested in the interval where
 .
.
Plugging these values into the Remainder Estimation Theorem formula, we get:
![\[|R_2(x)| = (e^c)/(6) \cdot \left((1)/(10)\right)^3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1wkm1urzki2bk1dwgpv4n65kvgxrbu068g.png)
To find the maximum error, we maximize
 . Calculating this expression gives us the final answer:
. Calculating this expression gives us the final answer:
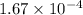 .
.
This means that the maximum error in the given interval is approximately
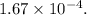
Complete Question:
The approximation ex = 1+x + x^2/2 is used when x is small. Use the Remainder Estimation Theorem to estimate the error when |x| < 1/10. Select the correct choice below and fill in the answer box to complete your choice. (Use scientific notation. Round to two decimal places as needed.)
A. The maximum error is approximately __ for M=1/10
B. The maximum error is approximately __ for M =1/e
C. The maximum error is approximately __ for M=1
D. The maximum error is approximately __ for M=2