Question

A 2.3 cm-tall object is placed 5.3 cm in front of a convex mirror with radius of curvature 24 cm. What is the image distance, in centimeters? Include its sign. What is the image height, in centimeters? Include its sign.

Answer 1

The image distance, considering the negative sign for its position behind the mirror, is approximately
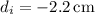`\(d_i = -2.2 \, \text{cm}\)`. The negative sign indicates that the image is formed behind the mirror, which is typical for virtual images produced by convex mirrors.

The image height, considering the positive value for its magnitude and its upright orientation, is approximately
`\(h_i = 0.952 \, \text{cm}\).`

For a convex mirror, we can use the mirror formula and magnification equation to find the image distance and image height.

The mirror formula for a convex mirror is:

`\[ (1)/(f) = (1)/(d_o) + (1)/(d_i) \]`

Where:

- f is the focal length of the mirror.

-
`\( d_o \)` is the object distance (given as -5.3 cm, as it is in front of the mirror).

-
`\( d_i \)` is the image distance (what we're solving for).

Given that the radius of curvature (R) is twice the focal length for a convex mirror:

`\[ f = (R)/(2) = \frac{24 \, \text{cm}}{2} = 12 \, \text{cm} \]`

Plugging in the values:

`\[ (1)/(12) = (1)/(-5.3) + (1)/(d_i) \]`

`\[ (1)/(d_i) = (1)/(12) - (1)/(-5.3) \]`

`\[ (1)/(d_i) = (1)/(12) + (1)/(5.3) \]`

`\[ (1)/(d_i) = (16.9 + 12)/(12 * 5.3) \]`

`\[ (1)/(d_i) = (28.9)/(12 * 5.3) \]`

`\[ d_i = (12 * 5.3)/(28.9) \]`

`\[ d_i \approx 2.2 \, \text{cm} \]`

The negative sign indicates that the image is formed behind the mirror, which is consistent with a virtual image formed by a convex mirror.

Now, to find the image height
`(\( h_i \))`, we use the magnification equation for mirrors:

`\[ \text{Magnification} = (h_i)/(h_o) = -(d_i)/(d_o) \]`

Given:

- Object height
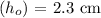`(\( h_o \)) = 2.3 cm` (positive as it's upright)

- Image distance
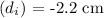`(\( d_i \)) = -2.2 cm` (negative as it's behind the mirror)

- Object distance
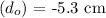`(\( d_o \)) = -5.3 cm` (negative as it's in front of the mirror)

`\[ (h_i)/(2.3) = -((-2.2))/(-5.3) \]`

`\[ (h_i)/(2.3) = (2.2)/(5.3) \]`

`\[ h_i = (2.2 * 2.3)/(5.3) \]`

`\[ h_i \approx 0.952 \, \text{cm} \]`

The negative sign indicates that the image is upright (same orientation as the object), which is typical for images formed by convex mirrors, and the image height is smaller than the object height.

Answer 2

The image distance is -9.5 cm and the height of the image is 4.12 cm.

How to calculate the image distance?

The image distance is calculated by applying the following formula as follows;

1/f = 1/u + 1/v

where;

• f is the focal length
• u is the object distance
• v is the image distance

The focal length = r/2

f = 24 cm / 2

f = 12 cm

1/12 = 1/5.3 + 1/v

1/v = 1/12 - 1/5.3

1/v = -0.1053

v = 1/(-0.1053)

v = -9.5 cm

The height of the image is calculated as;

M = Hi/h = v/u

Hi/2.3 = 9.5 / 5.3

Hi = 2.3 x (9.5/5.3)

Hi = 4.12 cm