Question

use a linear approximation (or differentials) to estimate the given number. (round your answer to five decimal places.) 3 sqrt(65)

Answer 1

To estimate 3 √(65), we use a linear approximation based on the easily computed 3 √(64) and apply differentials to find the change for x=65, resulting in an estimate of 24.18750.

Step-by-step explanation:

To estimate 3 √(65) using a linear approximation, we find a function that is easy to compute and close to our number of interest. Since √(64) is close to √(65) and easy to work with because 64 is a perfect square, we can use this value for our estimation. The function f(x) = 3√(x) at x = 64 can be used, and then we apply differentials to estimate the change for x = 65.

First, compute the derivative of f(x): f'(x) = (3/2)x^(-1/2). Then, evaluate this derivative at x = 64: f'(64) = (3/2)64^(-1/2) = 3/16. Now, use the differential df = f'(x)dx where dx = 1 since 65 - 64 = 1, so df = 3/16 * 1.

The linear approximation for f(65) is f(64) + df. Since f(64) = 3√(64) = 3 * 8 = 24 and the differential df = 3/16, we add these together to get 24 + 3/16 = 24.1875. When rounded to five decimal places, our estimate for 3 √(65) is 24.18750.

Answer 2

The approximate value of 3√65 using a linear approximation is 4.06251, rounded to five decimal places.

Choose a reference point, we chose 64, slightly smaller than 65, as our reference point.

Now, we have to calculate function value at the reference point, we get;

f(64) = 3√64

f(64) = 4

Calculating the derivative, we have;

f'(x) = (1/3) ×
`x^(^-^2^/^3^)`

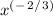
Evaluate the derivative at the reference point;

f'(64) ≈ 0.09375

Set up the linear approximation

y ≈ 4 + 0.09375 × (x - 64)

Estimate the value at x = 65, we get that;

y ≈ 4.0625

Therefore, the approximate value of 3√65 using a linear approximation is 4.0625, rounded to five decimal places.