Question

Find the area of the shaded segment of the circle

Answer 1

7.1 m²

Explanation:

The area of the shaded segment can be calculated by subtracting the area of the triangle from the area of the sector.

Angles around a point sum to 360°. Therefore, as the major arc of the given circle is 270°, the minor arc is 90°, since 360° - 270° = 90°.

In a circle, the measure of an arc is equal to the measure of its corresponding central angle. Therefore, the central angle of the sector is 90°.

Area of the sector

The formula for the area of a sector of a circle is:

`\large\boxed{\textsf{Area of Sector} = (\theta)/(360^(\circ)) \pi r^2}`

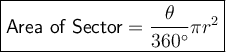
where:

• θ is the central angle of the sector (in degrees).
• r is the radius of the circle.

Given:

• θ = 90°
• r = 5 m

Substitute the values into the formula to calculate the area of the sector:

`\begin{aligned}\textsf{Area of the sector} &= (90^(\circ))/(360^(\circ)) \pi \cdot 5^2\\\\&= (1)/(4) \pi \cdot 25\\\\&= (25)/(4) \pi\; \sf cm^2\end{aligned}`

Area of the triangle

The triangle has two congruent sides of 5 m (radii) and an apex angle of 90°. This means it is a right triangle with congruent legs measuring 5 m. The legs are the base and height of the triangle.

The formula for the area of a triangle with base b and height h is:

`\large\boxed{\textsf{Area of a triangle}=(1)/(2)bh}`

Therefore, substitute b = 5 and h = 5 into the formula to calculate the area of the triangle:

`\begin{aligned}\textsf{Area of the triangle}&=(1)/(2)\cdot 5 \cdot 5\\\\&=(5)/(2)\cdot 5\\\\&=(25)/(2)\;\sf cm^2\end{aligned}`

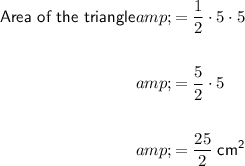
Area of the shaded segment

To find the area of the shaded segment, we can subtract the area of the triangle from the area of the sector:

`\begin{aligned}\textsf{Shaded segment}&=\sf Area_(sector)-Area_(triangle)\\\\&=(25)/(4)\pi-(25)/(2)\\\\&=19.634954...-12.5\\\\&=7.1349540...\\\\&=7.1\; \sf m^2\;(nearest\;tenth)\end{aligned}`

Therefore, the area of the shaded segment is 7.1 m² (rounded to the nearest tenth).