Question

The function is quadratic, and I need to find the diver's height after 1.75 secondds

Answer 1

usually we'd end up with a system of three variables by using three points to get the quadratic, but in this case since we have some zeros, we shamelessly used (0 , 48) to get one of the variables, so we only ended up with a system of two, not exactly but pretty much.

`{\Large \begin{array}{llll} y=ax^2+bx+c \end{array}} \\\\[-0.35em] ~\dotfill\\\\ (0~~,~~48)\hspace{5em}48=a(0)^2+b(0)+c\implies 48=c \\\\[-0.35em] ~\dotfill\\\\ (1~~,~~40)\hspace{5em}40=a(1)^2+b(1)+c\implies 40=a+b+c \\\\[-0.35em] ~\dotfill\\\\ (2~~,~~0)\hspace{5em}0=a(2)^2+b(2)+c\implies 0=4a+2b+c`

so from our template above, we get those three fellows, but the first equation gives us 48 = c, so we know what that is already, so let's shamelessly use it in the 2nd equation and then do some substitution

`\stackrel{\textit{substituting on the 2nd equation}}{40=a+b+(48)}\implies -8=a+b\implies -8-a=b \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{now doing some substituting on the 3rd equation}}{0=4a+2(-8-a)+(48)}\implies 0=4a-16-2a+48 \\\\\\ 0=2a+32\implies -32=2a\implies \cfrac{-32}{2}=a\implies \boxed{-16=a} \\\\\\ -8-a=b\implies -8-(-16)=b\implies \boxed{8=b}\hspace{5em}\boxed{c=48} \\\\[-0.35em] ~\dotfill\\\\ ~\hfill {\Large \begin{array}{llll} y=-16x^2+8x+48 \end{array}} ~\hfill`

`y(1.75)=-16(1.75)^2+8(1.75)+48\implies {\Large \begin{array}{llll} y(1.75)=13 \end{array}}`

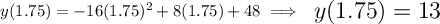
Check the picture below.