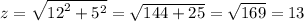Question

The hypotenuse of a right triangle is 1 cm longer than the longest leg. The shorter leg is 7 cm shorter than the longest leg. Find the dimensions of the triangle.

Answer 1

The hypotenuse is 13 cm

The longest leg is 12 cm

The shortest leg is 5 cm

Explanation:

Given:

A right triangle

Let's assume, that the longest leg is x, the shortest leg is y and the hypotenuse is z

Let's write 2 equations according to the given information and put them into a system (use the Pythagorean theorem):

`z = \sqrt{ {x}^(2) + {y}^(2) }`

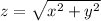
{√(x^2 + y^2) = x + 1,

{x - y = 7;

Let's make x the subject from the 2nd equation:

x = 7 + y

Replace x in the 1st equation with its value from the 2nd one:

`\sqrt{( {7 + y)}^(2) + {y}^(2) } = (7 + y) + 1`

`\sqrt{49 + 14y + {2y}^(2) } = 8 + y`

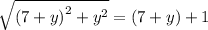
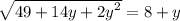
Square both sides of the equation:

`2 {y}^(2) + 14y + 49 = {(8 + y)}^(2)`

`2 {y}^(2) + 14y + 49 = 64 + 16y + {y}^(2)`

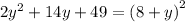
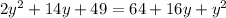
Move the expression to the left and collect like-terms:

`{y}^(2) - 2y - 15 = 0`

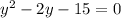
a = 1, b = -2, c = -15

Solve this quadratic equation:

`d = {b}^(2) - 4ac = ({ - 2})^(2) - 4 * 1 * ( - 15) = 64 > 0`

`y1 = ( - b - √(d) )/(2a) = (2 - 8)/(2 * 1) = ( - 6)/(2) = - 3`

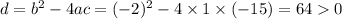
y must be a natural number, since the length of a triangle's side cannot have negative units

`y2 = ( - b + √(d) )/(2a) = (2 + 8)/(2 * 1) = 5`

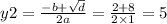
We found the length of the shortest leg

Now, we can find the rest of the dimensions:

x = 7 + 5 = 12

`z = \sqrt{ {12}^(2) + {5}^(2) } = √(144 + 25) = √(169) = 13`