Question

A 3.0-cm-tall object is 45 cm in front of a converging mirror that has a 25 cm focal length.

Part A Calculate the image position. Express your answer with the appropriate units. Enter positive value if the image is on the same side from the mirror and negative value if the image is on the other side.
s′ =
Part B Calculate the image height. Express your answer with the appropriate units.
h' =

Answer 1

Part A: The image position is approximately
`\(8.04 \, \text{cm}\)`. Since the object is in front of the mirror (real object), and the image distance is positive, it means the image is formed on the opposite side from the mirror.

Prat B: Therefore, the image height (h') is approximately
`\(0.5361 \, \text{cm}\)`.

Part A: For a converging mirror, the mirror equation relates the object distance (s), the image distance (s'), and the focal length (f):

`\[(1)/(f) = (1)/(s) + (1)/(s')\]`

Given:

Object height (h) = 3.0 cm (positive because it's an upright object)

Object distance (s) = -45 cm (negative because the object is in front of the mirror, which is the opposite direction of the light rays)

Focal length (f) = 25 cm

Let's first solve for the image position (s') using the mirror equation:

`\[(1)/(f) = (1)/(s) + (1)/(s')\]`

Plugging in the given values:

`\[\frac{1}{25 \, \text{cm}} = \frac{1}{-45 \, \text{cm}} + (1)/(s')\]`

Solving for s':

`\[(1)/(s') = \frac{1}{25 \, \text{cm}} - \frac{1}{-45 \, \text{cm}}\]`

`\[(1)/(s') = \frac{1}{25 \, \text{cm}} + \frac{1}{45 \, \text{cm}}\]`

`\[(1)/(s') = \frac{18}{225 \, \text{cm}} + \frac{10}{225 \, \text{cm}}\]`

`\[(1)/(s') = \frac{28}{225 \, \text{cm}}\]`

`\[s' = \frac{225 \, \text{cm}}{28}\]`

Calculating s':

`\[s' \approx 8.04 \, \text{cm}\]`

Part B: Now, let's calculate the image height (h') using the magnification formula:

`\[M = -(s')/(s)\]`

Given:

`\(s' = 8.04 \, \text{cm}\)`

`\(s = -45 \, \text{cm}\)`

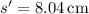
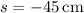
Calculating M:

`\[M = -\frac{8.04 \, \text{cm}}{-45 \, \text{cm}}\]`

`\[M \approx 0.1787\]`

The negative sign in the magnification indicates an inverted image.

Now, using the formula for magnification:

`\[M = (h')/(h)\]`

Given:

`\(h = 3.0 \, \text{cm}\)` (object height)

Calculating h':

`\[h' = M * h\]`

`\[h' = 0.1787 * 3.0 \, \text{cm}\]`

Calculating \(h'\):

`\[h' \approx 0.5361 \, \text{cm}\]`

Answer 2

(a) The position of the image is 56.25 cm.

(b) The height of the image is 3.75 cm.

How to calculate the image position?

(a) The position of the image is calculated by applying lens equation as follows;

1/f = 1/v + 1/u

where;

• f is the focal length
• v is the image position
• u is the object position

1/25 = 1/v + 1/45

1/v = 1/25 - 1/45

1/v = 0.0178

v = 1/0.0178

v = 56.25 cm

(b) The height of the image is calculated as;

M = Hi/h = v/u

Hi/3 = 56.25 / 45

Hi = 3 x (56.25/45)

Hi = 3.75 cm