Question

it is instructive to see how picard’s method works with a choice of the initial approximation other than the constant function y0(x) = y0. apply the method to the initial value problem (4) with (a) y0(x) =ex (b) y0(x) =1+x (c) y0(x) = cos x

Answer 1

The initial value problem of equivalent integral equation is:

• y(x) =
  `e^x` is y(x) = x²
• y(x) = 1+x is y(x) = 1+x+2[
  `e^x-x-1`]
• y(x) = cosx is given by y = -sinx - x +
  `(x^3)/(3!)` + 1 +x + x² + x³/3! + x⁴/3!

1) Given initial value problem is:

`(dy)/(dx) =x+y`

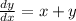
y(x) =
`e^x` , y = 1

The equivalent integral equation is,

`y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\`

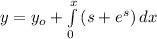
Then by pieard's method,

`y = 1 + \int\limits^x_0 {(s+e^s)} \, dx \\= 1+\int\limits^0_xsds+\int\limits^x_0 {e^s} \, dx`

`= 1+(x^2)/(2) +e^x`

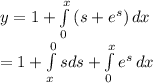
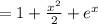
y(x) =
`e^(x^2)` -1

y(x) = x²

2) The given initial value problem is,

`(dy)/(dx) =x+y`

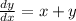
y(x) = 1+x

The equivalent integral equation is,

`y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\`

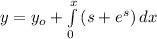
Then by pieard's method,

`y = 1 + \int\limits^x_0 {(s+1+s)} \, dx \\\\= 1+\int\limits^0_x {(1+2s)} \, dx \\= 1+[s]^x_0+2[(s^2)/(2) ]^x_0\\=1+x+x^2`

y(x) = 1+x+2[
`e^x-x-1`]

3) The given initial value problem is,

`(dy)/(dx) =cosx`

y(x) = cosx

The equivalent integral equation is,

`y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\`

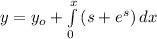
Then by pieard's method,

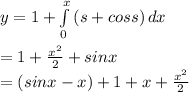
`y = 1 + \int\limits^x_0 {(s+cos s)} \, dx \\\\= 1+(x^2)/(2)+sinx \\ = (sinx-x)+1+x+(x^2)/(2)`

y = -sinx - x +
`(x^3)/(3!)` + 1 +x + x² + x³/3! + x⁴/3!

Leran more