Answer:
Approximately
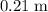 .
.
(Assuming that
 .)
.)
Step-by-step explanation:
As the bottle cap slows down, it lost kinetic energy
 :
:
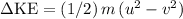 , where
, where
 is the mass of the cap,
is the mass of the cap,
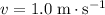 , and
, and
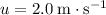 .
.
The amount of kinetic energy lost should also be equal to the sum of:
- gain in gravitational potential energy (
 ), and
), and - work that friction has done on the cap.
Let
 denote the distance that the cap has travelled along the ramp. The height of the cap would have increased by:
denote the distance that the cap has travelled along the ramp. The height of the cap would have increased by:
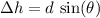 , where
, where
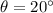 is the angle of elevation of the ramp.
is the angle of elevation of the ramp.
The
 of the cap would have increased by:
of the cap would have increased by:
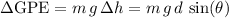 .
.
To find the friction on the cap, it will be necessary to find the normal force that the ramp exerts on the cap.
Let
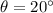 denote the angle of elevation of this ramp. Decompose the weight of the cap
denote the angle of elevation of this ramp. Decompose the weight of the cap
 (where
(where
 is the mass of the cap) into two directions:
is the mass of the cap) into two directions:
- Along the ramp:
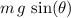 ,
, - Tangential to the ramp:
 .
.
The normal force on the cap is entirely within the tangential direction.
Since the cap is moving along the ramp, there would be no motion in the tangential direction. Forces in the tangential direction should be balanced. Hence, the normal force on the cap will be equal in magnitude to the weight of the cap in the tangential direction:
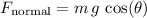 .
.
Since the cap is moving, multiply the normal force on the cap by the coefficient of kinetic friction
 to find the friction
to find the friction
 between the ramp and the cap:
between the ramp and the cap:
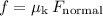 .
.
After a distance of
 along the ramp, friction would have done work of magnitude:
along the ramp, friction would have done work of magnitude:
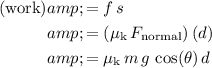 .
.
Overall:
 .
.
At the same time:
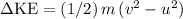 .
.
Therefore:
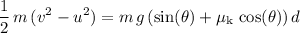 .
.
 .
.