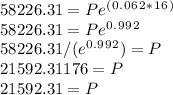Question

After 16 years in an account with a 6.2% annual interest rate compounded continuously, an investment is worth a total of $58,226.31. What is the value of the principal investment? Round the answer to the nearest penny.

$21,737.59
$21,592.31
$36634.00
$36488.72

Answer 1

Principal = $21,592.31

Explanation:

The formula for continuous compound interest is

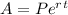`A = Pe^r^t`, where A is the amount (aka investment worth), r is the interest rate, and t is the time in years (the number e simply shows us that we're dealing with continuous compound interest)

Since we're already given that have A = $58,226.31, r = 0.062 (we must convert the percentage to a decimal by simply moving the decimal two places to the left, which is the same as dividing by 100), and t = 16 years, we can simply solve for P:

`58226.31=Pe^(^0^.^0^6^2^*^1^6^)\\58226.31=Pe^0^.^9^9^2\\58226.31/(e^0^.^9^9^2)=P\\21592.31176=P\\21592.31=P`