Question

Find the line of tangency to the circle defined by (x-3)^2 + (y-7)^2 = 169 at the point (15,2).

Answer 1

first off, let's look at the equation of the circle

`\textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \hspace{5em}\stackrel{center}{(\underset{}{h}~~,~~\underset{}{k})}\qquad \stackrel{radius}{\underset{}{r}} \\\\[-0.35em] ~\dotfill\\\\ (x-\stackrel{h}{3})^2+(y-\stackrel{k}{7})=169\implies (x-\stackrel{h}{3})^2+(y-\stackrel{k}{7})=\stackrel{ r }{13^2}`

so we have a circle centered at (3 , 7) with a radius of 13, Check the picture below.

so the line we want is the line in purple, which is tangential to the circle and therefore perpendicular to the blue line.

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the blue line

`(\stackrel{x_1}{3}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{15}~,~\stackrel{y_2}{2}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{2}-\stackrel{y1}{7}}}{\underset{\textit{\large run}} {\underset{x_2}{15}-\underset{x_1}{3}}} \implies \cfrac{ -5 }{ 12 } \implies - \cfrac{5 }{ 12 } \\\\[-0.35em] ~\dotfill`

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{ \cfrac{-5}{12}} ~\hfill \stackrel{reciprocal}{\cfrac{12}{-5}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{12}{-5} \implies \cfrac{12}{ 5 }}}`

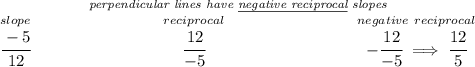
so we're really looking for the equation of a line whose slope is 12/5 and it passes through (15 , 2)

`(\stackrel{x_1}{15}~,~\stackrel{y_1}{2})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{12}{5} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{2}=\stackrel{m}{ \cfrac{12}{5}}(x-\stackrel{x_1}{15}) \\\\\\ y-2=\cfrac{12}{5}x-36\implies {\Large \begin{array}{llll} y=\cfrac{12}{5}x-34 \end{array}}`