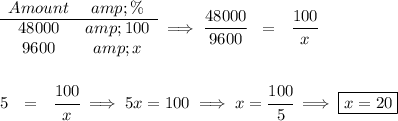Question

A salesman earns $60,000 in commission in his first year and then has his commission reduced by 20% the second year. What percent increase in commission over the second year will give him $57,600 in the third year?

Answer 1

first off, let's find out how much he's making on the 2nd year, so since he's getting slashed by 20%, that means his new commission is 100% - 20% = 80%, so 80% of 60000, how much is that?

`\begin{array}ll \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{80\% of 60000}}{\left( \cfrac{80}{100} \right)60000}\implies 48000`

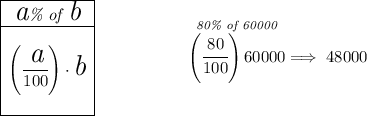
now, if we want to go up to 57600, that means we need to increase his commission by 57600 - 48000 = 9600.

So, if we take 48000(origin amount) to be the 100%, what's 9600 off of it in percentage?

`\begin{array}{ccll} Amount&\%\\ \cline{1-2} 48000 & 100\\ 9600& x \end{array} \implies \cfrac{48000}{9600}~~=~~\cfrac{100}{x} \\\\\\ 5 ~~=~~ \cfrac{ 100 }{ x }\implies 5x=100\implies x=\cfrac{100}{5}\implies \boxed{x=20}`