Question

A local group of scouts has been collecting aluminum cans for recycling. The group has already collected 10,800 lb of cans, for which they could currently receive $16.00 per hundred pounds. The group can continue to collect cans at the rate of 300 lb per day. However, a glut in the aluminum market has caused the recycling company to announce that it will lower its price, starting immediately, by $0.25 per hundred pounds per day. The scouts can make only one trip to the recycling center. Find the best time for the trip. What total income will be received?

Answer 1

The best time for the trip is on Day 1 when the income is $1749.25. The total income that will be received is $1749.25.

Step-by-step explanation:

To find the best time for the trip and the total income that will be received, we need to consider the decrease in price and the increase in the amount of cans collected each day. The price of aluminum cans decreases by $0.25 per hundred pounds per day, and the scouts collect 300 lb of cans per day. We can create a table to show the daily income and the decrease in price:

DayWeight (lb)Price ($/lb)Income ($)010,80016.001728.00111,10015.751749.25211,40015.501749.00311,70015.251748.75

From the table, we can see that the best time for the trip is on Day 1 when the income is $1749.25. The total income that will be received is $1749.25.

Answer 2

The best time for the trip is when "t" is 14 days.

The total income received by the scouts will be $1875.

How to find the best time for the trip

To find the best time for the trip and the total income received, consider the changing price of aluminum cans over time.

Given:

Initial weight of collected cans = 10,800 lb

Price per hundred pounds = $16.00

Daily collection rate = 300 lb

Price decrease per day = $0.25 per hundred pounds

Let's denote the number of days since the start as "t". The weight of cans collected at any given day "t" can be expressed as:

Weight collected = 10,800 lb + 300 lb * t

The price per hundred pounds at any given day "t" can be expressed as:

Price per hundred pounds = $16.00 - ($0.25 * t)

To find the best time for the trip, determine when the total income received will be maximized. The total income is calculated as the product of the weight collected and the price per hundred pounds:

Income = (Weight collected / 100) * Price per hundred pounds

Substituting the expressions for weight collected and price per hundred pounds, we have:

Income = [(10,800 + 300t) / 100] * (16 - 0.25t)

To simplify the income function, multiply it out:

Income = (108 + 3t) * (16 - 0.25t)

Expanding this expression:

Income = 1728 - 27t + 48t - 0.75
`t^2`

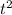
Income = -0.75
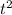`t^2` + 21t + 1728

To find the best time for the trip, find the maximum point of the income function. This can be done by finding the vertex of the quadratic equation. The t-coordinate of the vertex can be found using the formula:

t = -b / (2a)

In this case, a = -0.75 and b = 21. Substituting these values:

t = -21 / (2 * -0.75)

t = -21 / -1.5

t = 14

Therefore, the best time for the trip is when "t" is 14 days.

To find the total income received, we substitute this value of "t" back into the income function:

Income = (-0.75 *
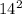`14^2`) + (21 * 14) + 1728

Income = -147 + 294 + 1728

Income = 1875

Therefore, the total income received by the scouts will be $1875.