Question

Let f(x)=x^2+3x-4. Find the number b such that the average rate of change of f on the interval [2,b] is 13.

Answer 1

I. Multiply the first function by the second one.

`f(x)* g(x) = (x^2+3x-4)*(x+4) = x^3 + 3x^2 - 4x + 4x^2 + 12x -16 = x^3 +7x^2 + 8x - 16`

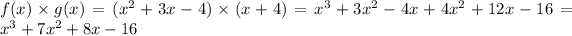
The domain of this new function is the set of all real numbers (R). Other notation: from minus infinity to plus infinity. We came to this conclusion because the new function poses no restrictions; regardless of which x-value you take, you will get the appropriate y-value.

II.
`f(x)/g(x) = (x^2+3x-4)/(x+4) =`

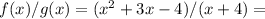
Ask yourself: which two numbers add up to 3 and multiply to -4? It's -1 and 4. Now we can represent
`f(x)` as
`(x-1)(x+4)`.

Since we're dividing these 2 brackets by
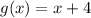`g(x)=x+4`, we may now cancel
`(x+4)`. All that's left is x-1.

The domain here is the same as in the previous task - it is R.