Question

Quadrilateral ABCD is inscribed in a circle. Find the measure of each of the angles of the quadrilateral. Show your work

Answer 1

x + 8 = 96, x - 4 = 84, 2x - 78 = 98

Explanation:

I did the test

Hope this helps :)

Answer 2

x + 8 = 96, x - 4 = 84, 2x - 78 = 98

Explanation:

See attached image.

All the angles are inscribed angles, so the measure of each one is 1/2 the measure of its intercepted arc.

Angle C intercepts arc BED. Angle E intercepts arc BCD. Those two arcs cover the entire circle. That means the measures of the arcs add up to 360.

`m\angle C + m\angle E =(1)/(2) m\text{ arc BED }+(1)/(2|)m\text{arc BCD} =(1)/(2)(360) =180 \\\\(x-4)+(x+8)=180 \\\\2x+4=180 \\\\2x=176 \\\\x=88`

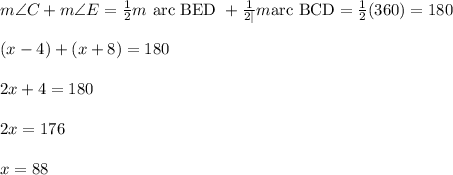
Substitute 88 for x in the expressions for the angle measures.