Question

For the function H(x)= -4x²-6x-4

write the function in vertex form

H(x) =

Answer 1

• 
  `H(x) = -4\bigg( x+(3)/(4)\bigg)^2 -(7)/(4)\\`

Explanation:

To find:-

• The vertex form of the given function.

Answer:-

The given function to us is,

`\longrightarrow H(x) = -4x^2 -6x-4 \\`

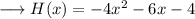
We are interested in finding out the vertex form, the vertex form is given by,

`\boxed{\begin{tabular}{c}\Large\bf{\underline{ Vertex \ Form }} \\\\ \large\textsf{ The Vertex form is given by :- } \\\\ \longrightarrow \boxed{H(x) = a(x-h)^2 + k }\\\\ \sf{ where,}\\ \\ \quad\qquad\qquad\qquad\bullet \textsf{ (h,k) is the vertex of the parabola. } \\\\ \bullet \textsf{ a is scaling factor. }\\\end{tabular}}`

Now we need to complete the square, this can be done by , firstly making coefficient of x² as 1 ,

`\longrightarrow H(x) = -4x^2 -6x-4\\`

`\longrightarrow H(x) = -4 \bigg(x^2 + (6)/(4)x + 1 \bigg) \\`

`\longrightarrow H(x) = -4\bigg\{ x^2 +2\bigg((3)/(4)\bigg)x + 1 \bigg\} \\`

`\longrightarrow H(x) = -4\bigg\{x^2+2\bigg((3)/(4)\bigg)x +\bigg((3)/(4)\bigg)^2-\bigg((3)/(4)\bigg)^2 + 1 \bigg\} \\`

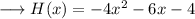
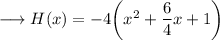
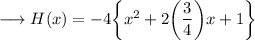
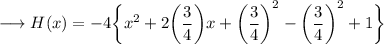
`\longrightarrow H(x) = -4\bigg[\bigg\{x^2+2\bigg((3)/(4)\bigg)x +\bigg((3)/(4)\bigg)^2\bigg\}-(9)/(16) + 1 \bigg]\\`

`\longrightarrow H(x) = -4\bigg\{ \bigg( x+(3)/(4)\bigg)^2 +(-9+16)/(16)\bigg\}\\`

`\longrightarrow H(x) = -4\bigg\{\bigg(x+(3)/(4)\bigg)^2+(7)/(16)\bigg\} \\`

`\longrightarrow \large\pmb{\underline{\boxed{H(x) = -4\bigg( x+(3)/(4)\bigg)^2 -(7)/(4)}}} \\`

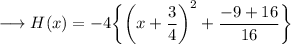
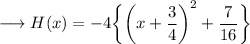
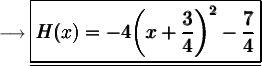
This is the required function in vertex form .

Also on comparing it to the standard vertex form , we get that,

• 
  `{\rm{ Vertex= \bigg(-(3)/(4),- (7)/(4) \bigg)= (-0.75,-1.75) }}`
• 
  `\rm a = -4`
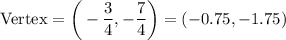
• Since the value of a is negative , the parabola will open downwards.

Graph for the same has been attached.