Question

If BE = 2x + 2, BD = 5x – 3, and AE = 4x – 6, what are the values of x and AC?

Answer 1

Answer: x=7 and AC = 44 unuts.

Explanation:

We know that the diagonals of a parallelogram bisect each other. (i)

Here in parallelogram ABCD , AC and Bd are diagonals intersecting at E.

BE = 2x + 2, BD = 5x – 3, and AE = 4x – 6

Using (i)

`BE=(BD)/(2)\\\\2x+2=(5x-3)/(2)\\\\ 2(2x+2)=5x-3\\\\ 4x+4= 5x-3\\\\ 5x-4x=4+3\\\\ x= 7`

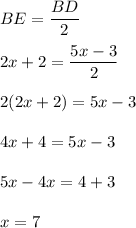
Now , AE = 4(7)-6 = 28-6 = 22

AC =2 AE = 2 (22) =44 units.

Hence, x=7 and AC = 44 unuts.