REFER TO PHOTO, WILL GIVE 90 POINTS

Question

asked May 1, 2024 18.6k views

1 Answer

Rafek · Answer 1 · 2024-05-05T09:01:06+0000

Answer:

Explanation:

To find:-

Answer:-

Let us take that, PQ = s , QS = p , QR = a and RS = b.

Here we can see that, ∆PQR and ∆PQS are right angled triangles .

Here, the value of RS would be,

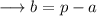
$\longrightarrow b = p - a \\$

Finding the value of "p" :-

In ∆PQS ,

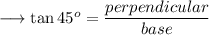
$\longrightarrow \tan 45^o =(perpendicular)/(base) \\$

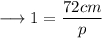
$\longrightarrow 1 = (72cm)/(p)\\$

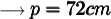
$\longrightarrow \large \pmb { p = 72cm }\\$

Finding the value of "a" :-

In ∆PQR , we can use Pythagoras theorem .

According to which, in a right angled triangle, the sum of squares of base and perpendicular is equal to the square of hypotenuse.
Hypotenuse is the longest side of the triangle and the side opposite to 90° is hypotenuse.

So that,

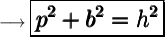
$\longrightarrow\Large \pmb{\boxed{ p^2 + b^2 = h^2 }}\\$

where the symbols have their usual meaning.

On substituting the respective values, we have;

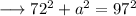
$\longrightarrow 72^2 + a^2 = 97^2 \\$

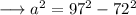
$\longrightarrow a^2 = 97^2-72^2 \\$

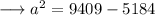
$\longrightarrow a^2 = 9409 - 5184 \\$

$\longrightarrow a^2 = 4225 \\$

$\longrightarrow a =√(4225)\\$

$\longrightarrow \large\pmb{ a = 65\ cm } \\$

Hence we can find the value of b as ,

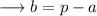
$\longrightarrow b = p-a \\$

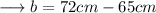
$\longrightarrow b = 72cm - 65cm\\$

$\longrightarrow b = 7cm \\$

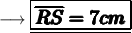
$\longrightarrow\large\pmb{\underline{\boxed{\pmb{ \overline{RS} = 7cm }}}}\\$

Therefore the value of RS is 7cm .