2 Answers

Miguel Ferreira · Answer 1 · 2024-12-06T22:15:14+0000

Sure, here's how to calculate the surface area of a rectangular prism with the given dimensions:

First, we can calculate the area of each face of the rectangular prism. The top and bottom faces each have an area of length times width, or lw:

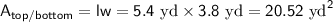
$\sf A_(top/bottom) = lw = 5.4\text{ yd} * 3.8\text{ yd} = 20.52\text{ yd}^2$

The front and back faces each have an area of height times width, or hw:

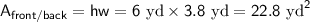
$\sf A_(front/back) = hw = 6\text{ yd} * 3.8\text{ yd} = 22.8\text{ yd}^2$

The left and right faces each have an area of length times height, or lh:

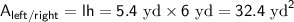
$\sf A_(left/right) = lh = 5.4\text{ yd} * 6\text{ yd} = 32.4\text{ yd}^2$

To find the total surface area of the rectangular prism, we add up the areas of all six faces:

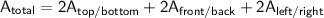
$\sf A_(total) = 2A_(top/bottom) + 2A_(front/back) + 2A_(left/right)$

Substituting in the values we calculated earlier, we get:

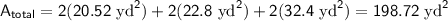
$\sf A_(total) = 2(20.52\text{ yd}^2) + 2(22.8\text{ yd}^2) + 2(32.4\text{ yd}^2) = 198.72\text{ yd}^2$

Therefore, the surface area of the rectangular prism is 198.72 square yards.

$\begin{align}\huge\colorbox{black}{\textcolor{yellow}{I hope this helps !}}\end{align}$

$\begin{align}\colorbox{purple}{\textcolor{lime}{Please mark as brillinest !}}\end{align}$

$\textcolor{cyan}{\small\textit{If you have any further questions, feel free to ask!}}$

RudyF · Answer 2 · 2024-12-10T14:35:24+0000

Answer:

-------------------------

Total surface area of a rectangular prism with dimensions of l, w and h is:

Given dimensions:

Substitute the values into the formula and calculate the toal surface area:

Please log in or register to add a comment.