Question

Type the correct answer in each box. If necessary, round your answer(s) to the nearest hundredth.

The vertices of AABC are A(-2, 2), B(6, 2), and C(0, 8). The perimeter of AABC is
units, and its area is
square units.

Answer 1

Sure! Here's how to find the perimeter and area of the given triangle using its vertices:

First, we can use the distance formula to find the lengths of the three sides of the triangle:

`\sf AB = √((6 - (-2))^2 + (2 - 2)^2) = √(64) = 8`

`\sf BC = √((0 - 6)^2 + (8 - 2)^2) = √(68) \approx 8.25`

`\sf CA = √((0 - (-2))^2 + (8 - 2)^2) = √(68) \approx 8.25`

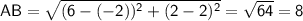
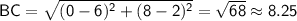
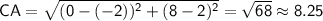
The perimeter of the triangle is the sum of these side lengths:

`\sf P = AB + BC + CA \approx 24.50`

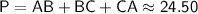
Next, we can use the coordinates of the three vertices to find the length of one side and the height of the triangle. We'll use side AB as the base of the triangle, and drop a perpendicular line from vertex C to side AB to find the height:

The length of AB is 8, and the height of the triangle can be found as follows:

`\sf \text{Slope of AB} = (2 - 2)/(6 - (-2)) = 0`

`\sf \text{Equation of AB} = y = 2`

`\sf \text{Equation of line through C perpendicular to AB: } x = 0`

`\sf \text{Height of triangle} = 8 - 2 = 6`

Therefore, the area of the triangle is:

`\sf A = (1)/(2)(\text{base})(\text{height}) = (1)/(2)(8)(6) = 24`

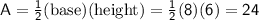
Rounding to the nearest hundredth, we get a perimeter of 24.50 units and an area of 24.00 square units.

`\begin{align}\huge\colorbox{black}{\textcolor{yellow}{I hope this helps !}}\end{align}`

`\begin{align}\colorbox{purple}{\textcolor{lime}{Please mark as brillinest !}}\end{align}`

`\textcolor{cyan}{\small\textit{If you have any further questions, feel free to ask!}}`