To solve for the second number given the GCF and LCM of two numbers and one of the numbers, we can follow the steps below:
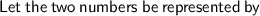 \:
\:
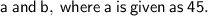
\text{We know that the GCF of } a \text{ and } b \text{ is 3, which means that 3 is a factor of both } a \text{ and } b.} \
\text{We also know that the LCM of } a \text{ and } b \text{ is 180, which means that } a \text{ and } b \
\text{have no common factors other than 3, and their product divided by 3 equals 180:} \
a \times b &= 3 \times \text{LCM}(a, b) \
&= 3 \times 180 \
&= 540 \
\text{Since we know that } a = 45, \text{ we can substitute this into the equation above to solve for } b: \
45 \times b &= 540 \
\text{Dividing both sides by 45, we get:} \
b &= 12 \
\end{align*}
Therefore, the second number is 12.
Answer: b=12