Question

Suppose Julio tosses a coin four times. What is the theoretical probability of tossing heads at least two times? Express your answer as a fraction in simplest form.

Answer 1

When a coin is tossed, there are two equally likely outcomes: heads or tails. Since Julio tosses the coin four times, there are a total of
`2 * 2 * 2 * 2 = 16` possible outcomes.

To determine the probability of tossing heads at least two times, we need to count the number of outcomes in which Julio gets two or more heads.

There are several ways to approach this problem, but one common method is to use the binomial distribution. If we let X be the number of heads that Julio gets in four tosses, then X follows a binomial distribution with parameters n = 4 (the number of trials) and p = 1/2 (the probability of getting heads on a single toss).

The probability of getting exactly k heads in four tosses is given by the binomial probability formula:

`\text{P(X = k) = (n choose k)} \ \text{p}^{\text{k}} (1 - p)^{\text{(n - k)}}`

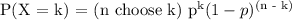
where
`\frac{\text{(n choose k)} = \text{n}!}{\text{(k! (n - k)!)}}` is the binomial coefficient, which gives the number of ways to choose k items from a set of n distinct items.

Using this formula, we can calculate the probability of getting two, three, or four heads in four tosses:

`\text{P(X = 2) = (4 choose 2)} \huge \text((1)/(2)\huge \text )^2 \huge \text((1)/(2) \huge \text)^2 = (6)/(16)`

`\text{P(X = 3) = (4 choose 3)} \huge \text((1)/(2)\huge \text )^3 \huge \text((1)/(2) \huge \text)^1 = (4)/(16)`

`\text{P(X = 4) = (4 choose 4)} \huge \text((1)/(2)\huge \text )^4 \huge \text((1)/(2) \huge \text)^0 = (1)/(16)`

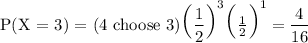
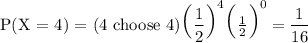
The probability of getting at least two heads is the sum of these probabilities:

`\text{P(X = 2) = P(X = 2) + P(X = 3) + P(X = 4)} = ((6 + 4 + 1))/(16) = (11)/(16)`

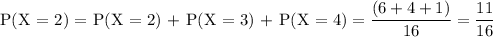
Therefore, the theoretical probability of tossing heads at least two times in four tosses is
`(11)/(16)`.