Question

Approximate sin(100) using the degree 3 Maclaurin polynomial for sin(x). Enter your answer as a simplified fraction. Notice how ridiculous this approximation is given that -1 sin(x) < 1 for any value of 1. sin(100) = ?

Answer 1

The approximation of
`\( \sin(100) \)` using the degree 3 Maclaurin polynomial is
`\( (-9700)/(3) \)`.

The Maclaurin series expansion for
`\( \sin(x) \)` is given by:

`\[ \sin(x) = x - (x^3)/(3!) + (x^5)/(5!) - (x^7)/(7!) + \ldots \]`

For the degree 3 Maclaurin polynomial, we consider the terms up to
`\( x^3 \)`:

`\[ \sin(x) \approx x - (x^3)/(3!) \]`

Now, substitute
`\( x = 100 \)` into this approximation:

`\[ \sin(100) \approx 100 - (100^3)/(3!) \]`

Let's calculate this:

`\[ \sin(100) \approx 100 - (100^3)/(6) \]`

Now, simplify the fraction:

`\[ \sin(100) \approx 100 - (100^2)/(3) \]`

Calculate
`\( 100^2 \)`:

`\[ \sin(100) \approx 100 - (10000)/(3) \]`

Now, find a common denominator:

`\[ \sin(100) \approx (300 - 10000)/(3) \]`

Combine the terms:

`\[ \sin(100) \approx (-9700)/(3) \]`

Complete the question:

Approximate sin(100) using the degree 3 Maclaurin polynomial for sin(x). Enter your answer as a simplified fraction. Notice how ridiculous this approximation is given that -1 sin(x) < 1 for any value of 1. sin(100) = ?/6. Find the value of ?

Answer 2

The ridiculous approximation for
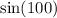`\( \sin(100) \)` using a degree 3 Maclaurin polynomial is
`\( -166566.67 \)`.

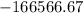The Maclaurin series expansion for
`\( \sin(x) \)` up to the degree 3 is given by:

`\[ \sin(x) \approx x - (x^3)/(6) \]`

To approximate
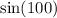`\( \sin(100) \)` using this polynomial, we substitute
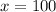`\( x = 100 \)` into the expression:

`\[ \sin(100) \approx 100 - (100^3)/(6) \]`

Calculating this, we get:

`\[ \sin(100) \approx 100 - (1000000)/(6) \]`

Simplifying the fraction yields:

`\[ \sin(100) \approx 100 - 166666.67 \]`

The result is approximately
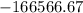`\(-166566.67\)`. However, given that the range of
`\( \sin(x) \)` is between -1 and 1, this approximation is indeed ridiculous. It violates the bounds imposed by the sine function, emphasizing the limitations of polynomial approximations, especially when extrapolating far beyond the region where the polynomial is derived.

In conclusion, the approximation
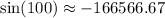`\( \sin(100) \approx -166566.67 \)` is absurd, showcasing the inaccuracy of polynomial approximations beyond their valid ranges.

The question probable maybe:

Approximate sin(100) using the degree 3 Maclaurin polynomial for sin(x) Notice how ridiculous this approximation is, given that - 1 <= sin(x) <= 1

sin(100)≈ ?/6 (your answer ? is an integer).