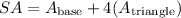Question

Use a net to find the surface area of the solid.

The surface area is
Explain your reasoning.
square units.

Answer 1

`SA = 133 \text{ square units}`

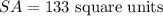
Explanation:

We can represent the surface area of a solid as the sum of the area of each of its sides, and we know that a square pyramid has 4 congruent triangles as sides and a square base.

We can first solve for the area of the square base.

`A_{\text{base}} = (\text{side length})^2`

`A_{\text{base}} = (7 \text{ units})^2`

`A_{\text{base}} = 49 \text{ square units}`

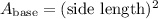
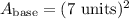
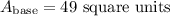
Next, we can solve for the area of the triangle sides.

Note that the height in this formula is the slant height of the pyramid.

`A_{\text{triangle}} = (1)/(2) \cdot \text{base} \cdot \text{height}`

`A_{\text{triangle}} = (1)/(2) \cdot (\text{7 units}) \cdot (\text{6 units})`

`A_{\text{triangle}} = 21 \text{ square units}`

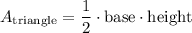
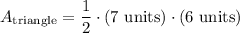
Finally, we can add the area of each side of the pyramid to get the total surface area of the solid. Remember that there are 4 triangle sides.

`SA = A_{\text{base}} + 4(A_{\text{triangle}})`

`SA = 49 \text{ square units} + 4(21 \text{ square units})`

`SA = 49 \text{ square units} + 84 \text{ square units}`

`\boxed{SA = 133 \text{ square units}}`