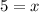Question

The two triangles are similar.

What is the value of x?

Answer 1

`x = 5`

Explanation:

We can solve for x using a proportion, since we are given that the two right triangles are similar. Here is the proportion modeled in an equation:

`(3x+1)/(12) = (4x)/(12 + 3)`

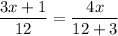
We can solve for x by algebraically manipulating this equation.

↓ simplifying the right fraction's denominator

`(3x+1)/(12) = (4x)/(15)`

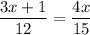
↓ cross-multiplying

`15(3x+1)= 12(4x)`

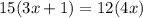
↓ applying the distributive property

`45x + 15 = 48x`

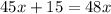
↓ subtracting
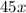`45x` from both sides

`15 = 3x`

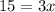
↓ dividing both sides by 3

`5 = x`

`\boxed{x = 5}`

Answer 2

x = 5

Explanation:

`(15)/(4x) = (12)/(3x + 1)`

`15(3x + 1) = 12(4x)`

`45x + 15 = 48x`

`3x = 15`

`x = 5`