Question

A small town has two local high schools. High School A currently has 1000 students and is projected to grow by 35 students each year. High School B currently has 700 students and is projected to grow by 55 students each year. Let A represent the number of students in High School A in t years, and let B represent the number of students in High School B after t years. Write an equation for each situation, in terms of t, and determine after how many years, t, the number of students in both high schools would be the same.

Answer 1

Sure, I can help you with that. Here are the equations for each situation:

* High School A:
`$A = 1000 + 35t$`

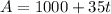
* High School B:
`$B = 700 + 55t$`

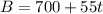
To determine after how many years, $t$, the number of students in both high schools would be the same, we can set the two equations equal to each other and solve for $t$. This gives us the equation:

`$1000 + 35t = 700 + 55t$`

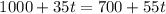
Solving for $t$, we get:

`$20t = 300$`

`$t = 15$`

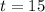
Therefore, after 15 years, the number of students in both high schools would be the same.

Explanation: