Need asap .............................. - QAmmunity.org

Need asap ..............................

asked Jan 1, 2024 202k views

2 Answers

Answer:

Explanation:

To find:-

The value of x.

Answer:-

From the given figure we can see that there are three right angled triangles namely ∆ACB , ∆BCD and ∆ACD .

To find out the value of x , we will have to use Pythagoras theorem . The Pythagoras theorem is ,

Pythagoras theorem:-

In a right angled triangle , the sum of squares of base and perpendicular is equal to the square of hypotenuse.

In a triangle hypotenuse is the longest side . In a right angled triangles, the side opposite to 90° will be hypotenuse.

Using Pythagoras theorem in ∆ACB :-

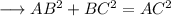
$\longrightarrow AB^2+BC^2= AC^2 \\$

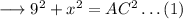
$\longrightarrow 9^2 + x^2 = AC^2 \dots(1)\\$

Using Pythagoras theorem in ∆BCD:-

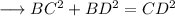
$\longrightarrow BC^2 + BD^2 = CD^2 \\$

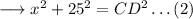
$\longrightarrow x^2+25^2 = CD^2 \dots(2) \\$

Using Pythagoras theorem in ∆ACD :-

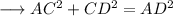
$\longrightarrow AC^2 + CD^2 = AD^2 \\$

Substituting the respective values from equations (1) and (2) ,

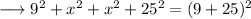
$\longrightarrow 9^2 + x^2 + x^2 + 25^2 = (9+25)^2 \\$

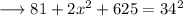
$\longrightarrow 81 + 2x^2 + 625 = 34^2 \\$

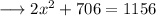
$\longrightarrow 2x^2 + 706 = 1156 \\$

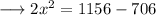
$\longrightarrow 2x^2 = 1156-706 \\$

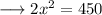
$\longrightarrow 2x^2 = 450\\$

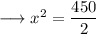
$\longrightarrow x^2 =(450)/(2)\\$

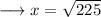
$\longrightarrow x = √(225) \\$

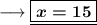
$\longrightarrow \underline{\boxed{\boldsymbol{ x = 15 }}} \\$

Therefore the value of x is 15 .

Need asap ..............................-example-1

Alexey Pelekh answered Jan 1, 2024

by Alexey Pelekh

7.9k points

← Prev Question Next Question →

Search QAmmunity.org