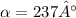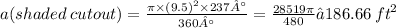Question

Find the area of the SHADED sector

186.66 ft.^2
387.49 ft^2
746.63 ft^2
96.87 ft^2

Answer 1

Answer:387.49ft^2

Explanation:

A Shaded sector that subtends an arc of 123 degrees in a circle of radius 19ft

A=(1/2)r^x

where x is the angle

A = (1/2)(19ft^2)(123*(22/7)/180)

=387.49ft^2

Answer 2

The first answer is correct

Explanation:

Given:

d (diameter) = 19 ft

The given angle of 123° is a central angle

Find: A (shaded area) - ?

Since the whole circle forms an angle of 360°, the remaining angle (of the shaded area) is:

`360° - 123° = 237°`

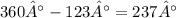
Now we can find the shaded cutout area by using this formula:

`a(cutout) = \frac{\pi * {r}^(2) * \alpha }{360°}`

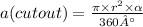
r = 0,5 × d = 0,5 × 19 = 9,5 ft

`\alpha = 237°`

`a(shaded \: cutout) = \frac{\pi * ( {9.5})^(2) * 237°}{360°} = (28519\pi)/(480) ≈186.66 \: {ft}^(2)`