Question

Suppose f(x) = x2 and g(x) = (1/4x)^2

graph of g(x) with the graph of f(x)?
2
.Which statement best compares the
O A. The graph of g(x) is the graph of f(x) vertically stretched by a
factor of 4.
• B. The graph of g(x) is the graph of f(x) horizontally stretched by a
factor of 4.
O c. The graph of g(x) is the graph of (x) horizontally compressed by a
factor obA.
O D. The graph of g(x) is the graph of Mx) shifted } units right.

Answer 1

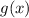`g(x)` is the image of
`f(x)` after stretched horizontally by scale factor = 4

Explanation:

The statement that best compares the graph of
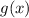`g(x)` with the graph of
`f(x)` says
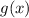`g(x)` is the image of
`f(x)` after stretched horizontally by scale factor = 4 because:

Given the function

`f(x) = x^2` and
`g(x) = ((1)/(4) x)^2` the image of
`f(x)` after one transformation.

The transformation shows that
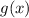`g(x)` stretches away from y-axis.

Since the transformation is stretched horizontally. So
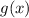`g(x)` is the image of
`f(x)` after stretched horizontally by scale factor (I.e. by 1).

Then we use the scale factor to divide
`g(x)`

`1 / (1)/(4) = 1 * (4)/(1) = 4`

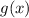
So therefore,
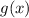`g(x)` is the image of
`f(x)` after stretched horizontally by scale factor = 4