Question

,

The value of the electric field at a distance
of 60.7 m from a point charge is 61.9 N/C and
is directed radially in toward the charge.
What is the charge? The Coulomb constant
is 8.98755 × 10^9 N · m^2/C^2
.
Answer in units of C.

Answer 1

Approximately
`(-2.54) * 10^(-5)\; {\rm C}`.

Step-by-step explanation:

The magnitude of the electric field around a point charge can be found with the equation:

`\begin{aligned} E &= (k\,q)/(r^(2))\end{aligned}`, where:

• 
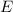  `E` is the magnitude of the electric field,
• 
  `k = 8.98755 * 10^(9)\; {\rm N\cdot m^(-2)\cdot C^(-2)}` is the Coulomb constant,
• 
  `q` is the magnitude of the point charge, and
• 
  `r = 60.7\; {\rm m}` is the distance from the point charge.

Rearrange this equation and solve for the magnitude
`q` of this point charge:

`\begin{aligned}q &= (r^(2)\, E)/(k) \\ &= ((60.7)^(2)\, (61.9))/(8.98755)\; {\rm C} \\ &\approx 2.54* 10^(-5)\; {\rm C}\end{aligned}`.

Note that the sign of electric charges can be either positive or negative. The direction of field lines around this point charge provides info on the sign of this electric charge.

By convention, the direction of electric field lines at a particular position is the same as the direction of the force on a positive electric test charge at that location. Since the electric field around this point charge points towards the charge, it means a positive charge would be attracted to this point charge.

Charges of opposite signs attract each other. For the point charge in this question to attract a positive test charge, it must be true that this point charge has a negative sign. Hence, this point charge would be
`(-2.54) * 10^(-5)\; {\rm C}`.