Answer:
The monkey hit the pond after approximately
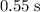 in the air.
in the air.
The monkey hit the pond approximately
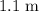 away from the base of the cliff.
away from the base of the cliff.
(Assume that
 , air resistance on the monkey is negligible, and the cliff is vertical.)
, air resistance on the monkey is negligible, and the cliff is vertical.)
Step-by-step explanation:
Assume that the air resistance on the monkey is negligible. The vertical acceleration of the monkey would be constantly
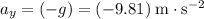 . Note that
. Note that
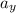 is negative since the monkey is accelerating downwards.
is negative since the monkey is accelerating downwards.
Right before hitting the pond, the monkey would be
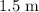 below the cliff. Hence, the vertical displacement
below the cliff. Hence, the vertical displacement
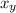 of the monkey would be
of the monkey would be
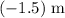 .
.
Let
 denote the initial vertical velocity of the monkey. Since the top of the cliff is level, initial velocity will be entirely horizontal. Hence,
denote the initial vertical velocity of the monkey. Since the top of the cliff is level, initial velocity will be entirely horizontal. Hence,
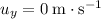 .
.
Let
 denote the amount of time it took for the monkey to hit the pond (
denote the amount of time it took for the monkey to hit the pond (
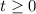 .) Rearrange the SUVAT equation
.) Rearrange the SUVAT equation
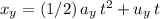 and solve for
and solve for
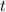 .
.
Since
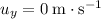 , the equation simplifies to:
, the equation simplifies to:
 .
.
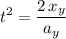 .
.
Since
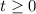 :
:
 .
.
Hence, it would take approximately
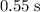 for the monkey to hit the pond.
for the monkey to hit the pond.
Also because air resistance on the monkey is negligible, the horizontal velocity
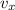 of the monkey will be constantly equal to the initial value
of the monkey will be constantly equal to the initial value
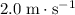 .
.
Hence, the monkey would have travelled a horizontal distance
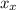 of:
of:
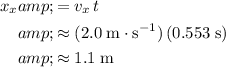 .
.