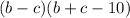Question

B^2-c^2-10(b-c) factor completly

Answer 1

`(b - c)(b + c - 10)`

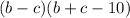
Explanation:

`{b}^(2) - {c}^(2) - 10(b - c)`

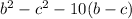
What does factorising mean?

• Factorising is a way of writing an expression as a product of its factors using brackets

What does expanding brackets mean?

• Expanding brackets is multiplying every term inside the bracket by the term on the outside (remember, if you multiply a negative number by another negative number, the product will be positive)

Now, expand the brackets in this expression:

`{b}^(2) - {c}^(2) - 10b + 10c`

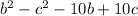
Apply the difference of squares formula to factor the expression even more (also, factor out -10 from the expression by putting it in front of the brackets):

`(b - c)(b + c) - 10(b - c)`

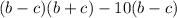
Now, factor out (b - c) from the expression:

`(b - c)(b + c - 10)`