Question

A charity organization had a fundraiser where each ticket was sold for a fixed price. After selling

200
200200 tickets, they had a net profit of
$
12
,
000
$12,000dollar sign, 12, comma, 000. They had to sell a few tickets just to cover necessary production costs of
$
1
,
200
$1,200dollar sign, 1, comma, 200.
Let
�
yy represent the net profit (in dollars) when they have sold
�
xx tickets.
Which of the following could be the graph of the relationship?
Choose 1 answer:

Answer 1

The net profit can be calculated by subtracting the production costs from the total revenue generated by selling tickets. Since each ticket was sold for a fixed price, we can assume that the relationship between the net profit and the number of tickets sold is linear.

We know that when 200 tickets were sold, the net profit was $12,000, which means that the slope of the linear function is:

`\text{slope = (net profit at 200 tickets - net profit at 0 tickets)} / (200 - 0)`

`\text{slope} = (\$12,000 - \$1,200) / 200`

`\text{slope} = \$55`

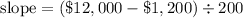
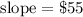
The y-intercept of the linear function represents the net profit when no tickets have been sold, which is equal to the negative of the production costs:

`\text{y-intercept} = -\$1,200`

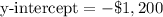
Therefore, the equation of the linear function is:

`\text{y} = \$55x - \$1,200`

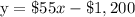
where x is the number of tickets sold and y is the net profit in dollars.

The graph of this function is an increasing linear function in quadrant 1 with a positive y-intercept, which is choice A. Therefore, the answer is choice A: graph of an increasing linear function in quadrant 1 with a positive y-intercept.