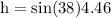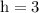Question

A pilot is flying over a straight highway. He determines the angles of depression to two mileposts,

6.7 km apart, to be 38° and 41°, as shown in the figure.
A
NOTE: The picture is NOT drawn to scale.
38°
6.7 km
41°
B
What is the elevation of the plane in meters? Give your answer to the nearest whole number.
height=
meters

Answer 1

a) 4.46 miles

b) 3 miles

Explanation:

Law of Sines:

`\frac{\text{a}}{\text{sin(A)}} =\frac{\text{b}}{\text{sin(B)}}`

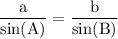
a) The distance of the plane from point A

The angle of depression corresponds to the congruent angle of elevation therefore, 180 - 28 - 52 = 100°

`\frac{\text{6.7}}{\text{sin(100)}} =\frac{\text{b}}{\text{sin(41)}}`

`\text{b}=\frac{6.7\text{sin}(41)}{\text{sin}(100)}`

`\text{b}=4.46 \ \text{miles}`

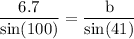
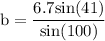
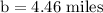
b) Elevation of the plane

`\text{sin}=\frac{\text{opposite}}{\text{hypotenuse}}`

hypotenuse is 4.46 and opposite is the elevation(h) to be found

`\text{sin}(38)=\frac{\text{h}}{4.46}`

`\text{h}=\text{sin}(38)4.46`

`\text{h}=3`