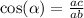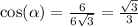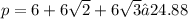Find Cos α, find x, and find perimeter

Question

asked Mar 5, 2024 582 views

1 Answer

Kevin Sitze · Answer 1 · 2024-03-09T23:33:03+0000

Answer:

1. x ≈ 15,73

P = 104,96

.

2. x ≈ 50,51

P = 136,26

.

3.

$\cos( \alpha ) = ( √(3) )/(3)$

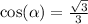
P ≈ 24,88

Explanation:

1.

Use trigonometry:

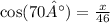
$\cos(70°) = (x)/(46)$

Cross-multiply to find x:

$x = 46 * \cos(70°) ≈15.73$

In order to find the perimeter, we have to know all three side lengths of the triangle

Let's find the third one by using the Pythagorean theorem:

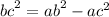
${bc}^(2) = {ab}^(2) - {ac}^(2)$

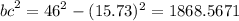
${bc}^(2) = {46}^(2) - ({15 .73})^(2) = 1868.5671$

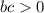
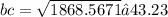
Now, we can find the perimeter (the sum of all side lengths):

P = AB + BC + AC

P = 46 + 43,23 + 15,73 = 104,96

.

2.

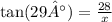
$\tan(29°) = (28)/(x)$

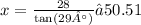
$x = (28)/( \tan(29°) ) ≈50.51$

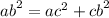
${ab}^(2) = {ac}^(2) + {cb}^(2)$

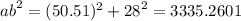
${ab}^(2) =( {50.51})^(2) + {28}^(2) = 3335.2601$

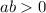
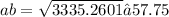
P = 57,75 + 28 + 50,51 = 136,26

.

3.

$\cos( \alpha ) = (ac)/(ab)$

$\cos( \alpha ) = (6)/(6 √(3) ) = ( √(3) )/(3)$