Question

Verify the identity so that the left side looks like the right side.


`(1+csc(x))/(cot(x)+cos(x))=sec(x)`

Answer 1

Let's see

LHS

`\\ \sf\longmapsto (1+csc(x))/(cot(x)+cos(x))`

• bring all into sine cosine form

`\\ \sf\longmapsto (1+(1)/(sin(x)))/((cos(x))/(sin(x))+cos(x))`

`\\ \sf\longmapsto \frac{\frac{1+sin(x)}{\cancel{sin(x)}}}{\frac{cos(x)+sin(x)cos(x)}{\cancel{sin(x)}}}`

`\\ \sf\longmapsto (1+sinx)/(cosx(1+sinx))`

`\\ \sf\longmapsto (1)/(cosx)`

`\\ \sf\longmapsto sec(x)`

verified

Answer 2

See below for proof.

Explanation:

Given expression:

`\implies (1+\csc(x))/(\cot(x)+\cos(x))`

`\boxed{\begin{minipage}{4.3 cm}\underline{Trigonometric Identities}\\\\$\csc(x)=(1)/(\sin(x))$\\\\\\$\cot(x)=(\cos(x))/(\sin(x))$\\\\\\$\sec(x)=(1)/(\cos(x))$\\\\\end{minipage}}`

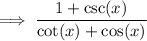
Use the trigonometric identities to rewrite csc(x) and cot(x) in terms of sin(x) and cos(x):

`\implies (1+(1)/(\sin(x)))/((\cos(x))/(\sin(x))+\cos(x))`

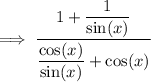
Simplify the numerator and denominator:

`\implies ((\sin(x)+1)/(\sin(x)))/((\cos(x)+\sin(x)\cos(x))/(\sin(x)))`

`\textsf{Apply the fraction rule:} \quad ((a)/(b))/((c)/(b))=(a)/(c)`

`\implies (\sin(x)+1)/(\cos(x)+\sin(x)\cos(x))`

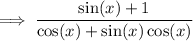
Factor out cos(x) from the denominator:

`\implies (\sin(x)+1)/(\cos(x)(1+\sin(x)))`

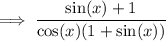
Cancel the common factor (1 + sin(x)):

`\implies (1)/(\cos(x))`

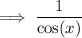
Rewrite 1/cos(x) using the identity:

`\implies \sec(x)`

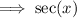
Therefore, the equation has been verified.